-
Calculation of electrostatic forces in presence of dielectrics
-
Calculation of electrostatic forces in presence of dielectrics
Created by Zoltan Losonc (feprinciples@on.mailshell.com)
There are two main methods for the calculation of electrostatic forces upon bodies both having their own advantages and disadvantages. The first is the direct method, when the macroscopic resultant force upon a body is calculated directly based on Coulomb’s law by summing up the elementary electrostatic forces acting on it. Its advantage is that it will give always correct result, but its disadvantage is that in most cases it is very difficult or even impossible to perform the calculation.
The second is an indirect method based on the assumed validity of the energy preservation law, when the forces are derived indirectly from energy correlations. The advantage of this method is that the forces can be calculated easily even by analytical methods. Its disadvantage is that the derived results are valid only if the law of energy preservation is also valid for that specific case. However this condition is not always satisfied and consequently this method can lead us to false results and conclusions in some cases. Although the representatives of the official science are firmly convinced that the law of energy preservation has a general validity, and therefore this method should provide always correct results, I would suggest to use it with due circumspection and reservation, always verifying the results when suspecting them to be wrong.
Forces on the plates of a flat capacitor calculated with direct method
As an example let us calculate the force that is pulling the plates of a flat condenser together, with the direct method (fig. 7a).
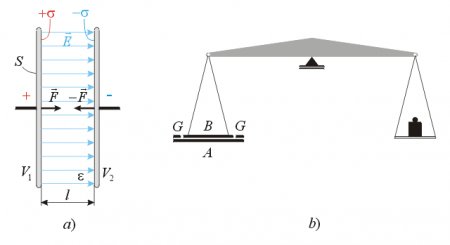
Fig. 7.
A simple analytical solution is possible only when the distance between the plates is much smaller than the size of the plates, because only in that case can we approximate the E-field between the electrodes to be homogeneous, and neglect the effect of the inhomogeneous E-field at the edges. With such initial approximation we can assume that there is no E-field outside the condenser, but only between the plates, where it has the same intensity and direction everywhere. To calculate the electrostatic forces upon a conductor we use the formula
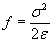 that has been derived from the Coulomb forces
F=qE here. Before calculating the electrostatic pressure, we
have to find the charge density s on the
inner surfaces of the electrodes:
that has been derived from the Coulomb forces
F=qE here. Before calculating the electrostatic pressure, we
have to find the charge density s on the
inner surfaces of the electrodes: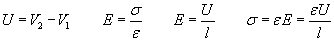
thus the force density (force per surface area):
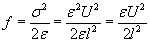
We get the total force that pulls one plate towards the other by multiplying the force density (electrostatic pressure) f with the surface area of the plate S:
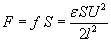
This force can be measured and verified experimentally with a sensitive ‘electrometer’ (W. Thomson, Kirchoff around 1880) as shown on fig. 7b; or when the voltage is unknown and the force is measured, then the voltage can be calculated from the above formula. The two main electrodes A and B are made of metal discs, and the upper smaller electrode A is surrounded with a protective ring GG that is kept at the same potential as the plate B to eliminate the edge-effect and ensure a homogeneous E-field between the plates A and B.
Forces on the plates of a flat capacitor calculated with indirect method
Now let’s see how can we derive the same formula with the indirect method by assuming the validity of energy preservation for this case, and deriving the force from energy correlations. Since there is an attractive force between the plates, when we increase the distance l between the plates with a very small distance dl, then we will have to perform a work of Fdl against the attractive force F (fig. 8a).
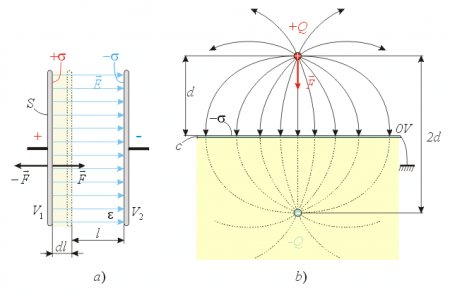
Fig. 8.
According to the energy preservation this invested mechanical work will increase the electrical energy stored within the condenser with dW=Fdl. Thus from this correlation we get the force:
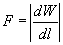 . Substituting
. Substituting 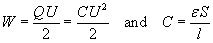 we get:
we get: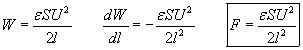
This result is the same as in the previous case that confirms the validity of energy preservation in this case. The negative sign means only that when the electric energy of the capacitor increases, then we will have to invest external mechanical energy to counteract the electric forces.
We have not specified whether the capacitor is in air or surrounded with some other liquid or solid dielectric, because the obtained formula is valid for all homogeneous and isotropic dielectrics, if we substitute their absolute dielectric constants. It is interesting to calculate these forces for different dielectrics and observe that when the voltage is kept constant we get more intense force for high permittivity dielectrics.
However when the charge is kept constant (the charged capacitor is disconnected from the power supply before moving the plates):
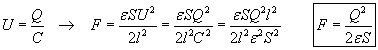
the force is greater for low permittivity dielectrics. This formula shows a constant force that is independent from the distance between the plates, however this is true only as long as our initial approximate assumption is satisfied, namely that the distance between the plates is much smaller than the size of the plates.
Force effect of neutral conductive surfaces upon nearby charges
Using the method of ‘mirror images’ to simplify calculations it is possible to reduce some seemingly complex electrostatic problems to simple analytic calculation.One such example is shown on fig. 8b, when a positive point charge +Q is placed at a distance d above a very big grounded conductive surface c. The charge +Q will influence an inhomogeneously distributed negative surface charge on the plate -s , thus it would be a complex task to calculate the attractive forces between the point charge and the plate based on this inhomogeneous charge distribution. We know that the E-field lines are always perpendicular to the surface of a conductor in electrostatics, and consequently the plate represents a kind of symmetry plain. If we mirror the picture of charge Q and the E-field lines below this symmetry plain changing the polarity of the mirrored charge-image to be negative, then the force can be calculated in a simplified way as the attractive Coulomb force between a positive and a negative point charge being at distance 2d from each other
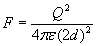 as shown on fig. 8b. This example has been chosen to illustrate the influence of conductive surfaces near highly charged bodies upon electric forces. In precise electrostatic measurements these ‘mirror forces’ should be taken into account even if the surrounding surfaces are not considered to be part of the active measurement setup.
as shown on fig. 8b. This example has been chosen to illustrate the influence of conductive surfaces near highly charged bodies upon electric forces. In precise electrostatic measurements these ‘mirror forces’ should be taken into account even if the surrounding surfaces are not considered to be part of the active measurement setup.Johnson – Rahbeck effect
Although the electrostatic forces are generally relatively weaker than the similar magnetic forces, we can still create significant force with an appropriate choice of the capacitor’s parameters. The obtained formula shows that when the voltage of the capacitor is kept constant the attractive force between the plates can be increased to very high intensity if the distance l is decreased. The only difficulty might be only in practical realizations of extremely small distances without shorting the circuit, or causing the breakdown of the dielectric, resulting in high short-circuit currents and drop of voltage.
An interesting practical realization of such capacitor is shown on fig. 9. The upper electrode is made of a semiconductive material Sc (ex. slate) coated with metal A on its upper surface, and the other electrode is made of metal M. When the precisely polished facing surfaces of the semiconductor and metal is placed upon each other and a voltage of U~100V is applied to the electrodes, they will stick to each other with great force. The reason for this is that the plates contact each other only in few points and thus only a weak current will flow through these contacts, thus there will be a very thin air gap (d ~10-3 - 10-4 mm) between the electrodes, and the very intense E-field (E ~ U/d) will create an intense attractive force. Although there is electric contact between the semiconductor and the metal electrode, the current I will be small due to the high contact resistance and high specific resistance of the semiconductor. This phenomenon is called Johnson – Rahbeck effect (1917) and it is utilized in electrostatic clutches and clamps.
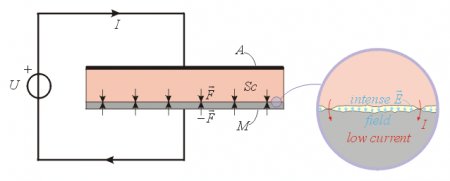
Fig. 9.
Two different dielectric layers in series between the plates of a flat capacitor
Now let’s examine a flat capacitor containing two layers of different dielectrics, when the boundary surface between the dielectrics is parallel with the plates. In this case the E-field intensities will not be the same in both dielectrics. To calculate the E-field intensities we can use the handy rule of electrostatics that says:
“The normal components of the electric displacement vectors D are equal on both sides of the boundary surface between different dielectrics” fig. 10:
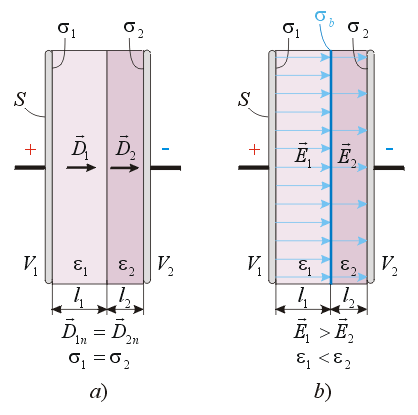
Fig. 10.
In the case of homogeneous and isotropic dielectrics the electric displacement vector is
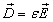 thus we get the E-field intensities as:
thus we get the E-field intensities as: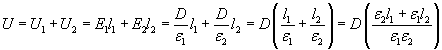
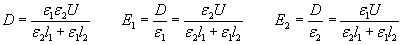
These formulas show that the E-field intensity is greater in the dielectric of lower permittivity e .
Now let’s turn to our main interest, and examine the electrostatic forces upon the capacitor shown on fig. 11. The formula for the electrostatic pressure
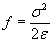 can be also written in the following forms:
can be also written in the following forms: 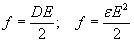 . Thus the force upon the left electrode is:
. Thus the force upon the left electrode is: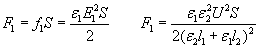
The force upon the right electrode can be calculated in similar way to get the result:
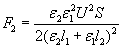
These formulas show that the force is greater on the plate, which is covered with the dielectric of less permittivity, and we might think that consequently there would be a resultant unidirectional reaction-less force upon the capacitor. However this is not true, since there are non-compensated bound surface charges sb on the boundary surface between the two dielectrics, and we have to take into account also the force acting on this boundary surface. To calculate this force we take advantage of a simple principle of electrostatics that says:
“When a very thin conductive surface is placed upon an equipotential surface, the E-field will remain the same and undisturbed”.
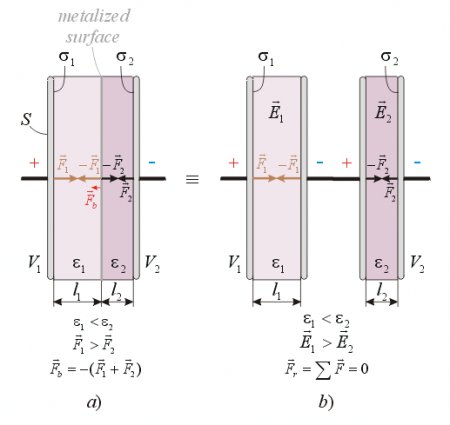
Fig. 11.
An equipotential surface is always perpendicular to the E-field lines. Since the boundary surface between the dielectrics is also perpendicular to E-field lines, it is also an equipotential surface. Now if we place a very thin metal plate on that surface between the two dielectrics, we practically get two capacitors connected in series, both filled with different dielectric as shown on fig. 11b. It is easy to recognize that the force on the left side of the boundary surface will be the same as –F1 and on its right side the same as –F2 as calculated above. Thus the resultant force upon this boundary layer will be Fb=F1 – F2:
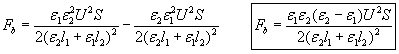
that has the same intensity but opposite orientation as the resultant force upon the two main electrodes. Consequently there will be no unidirectional resultant force upon the whole condenser. The direction of the resultant force upon the boundary layer is such that it wants to fill the whole condenser with the dielectric of greater permittivity. The same results can be derived with the indirect method from energy correlations.
Two different dielectric layers in parallel between the plates of a flat capacitor
Let’s take another example, when there are two different dielectrics between the plates, but the boundary surface between the dielectrics is perpendicular to the plates (fig. 12.)
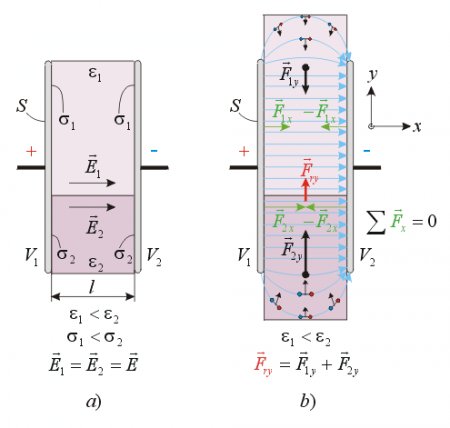
Fig. 12.
In this case we can use the following rule:
“The tangential components of the E-field intensities are identical on both sides of the boundary surface between two dielectrics.”
It is easy to realize that this must be so, since U=E1l=E2l thus E1=E2. Although the E-field intensities are identical, the electric displacement D and surface charge densities s on the plates touching the different dielectrics will be different (fig. 12a):
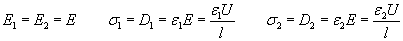
Since the E-field lines are parallel with the boundary surface, there can be no induced bound surface charges there, and consequently no electric force can act on that boundary surface. Examining the forces upon the plates we can see that there can not be any resultant unidirectional force in x direction upon the capacitor, because the forces in x direction are the same on both plates having opposite directions, thus canceling each other (fig. 12b).
After concluding that there is no electric force upon the boundary layer, we might get the idea to disconnect the capacitor from the power supply and move this surface in such direction to fill the whole capacitor with the dielectric of lower permittivity without mechanical resistance. Then the capacitance will be decreased and the electric energy stored in the condenser increased. If we could do this without mechanical resistance, then free energy could be produced in this way. However if we take a look at the shape of the E-field at the edges (fig. 12b), then we can recognize the force effects upon the dielectrics due to the arced inhomogeneous E-field, discussed on the previous pages. These forces will tend to pull both dielectrics into the capacitor, but since the elementary dipoles are bigger in the dielectric of higher permittivity, greater force will act on this dielectric than on the other. The macroscopic effect is again that the forces at the edges tend to fill the capacitor with the dielectric of higher permittivity.
Let us calculate the resultant force upon the dielectrics in y direction with the indirect method (fig. 13a).
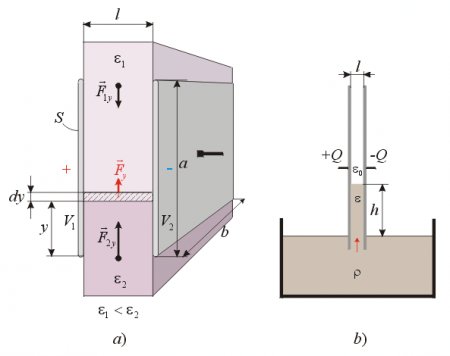
Fig. 13.
This type of capacitor can be considered as two capacitors with different dielectrics connected in parallel. Thus the resultant capacitance of the whole condenser will be the sum of these two partial capacitances:
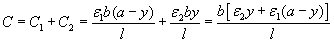
The electric energy contained in the condenser is:
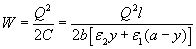
The electric energy change per distance of movement when the dielectrics are moved in y direction:
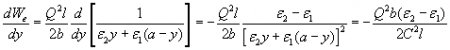
substituting
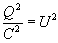 we get finally that:
we get finally that: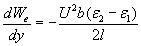
The resultant force upon the dielectrics is:
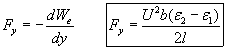
When e2>e1 then Fy is directed upwards trying to pull the dielectric of higher permittivity into the capacitor.
Electrostatic pump
This phenomenon can be nicely demonstrated with an experiment as shown on fig. 13b. If the bottom edge of a charged flat capacitor with air between the plates is merged in a liquid dielectric, then the above-discussed forces will push the liquid up between the plates against the force of gravity. When the electrical and gravitational forces are in equilibrium, then the upward movement of the dielectric between the plates stops, and the surface of the liquid within the capacitor will remain at a higher level than the liquid in the container. It is interesting to see how high can we lift up the liquid column for different parameters of the experimental setup. The level of the dielectric will move upwards as long as the weight of the liquid column does not become equal with the above-calculated electric forces. The weight of the dielectric column is: G =r h b l g, (r - is the density of the liquid; g – is the gravitational acceleration). When the two forces are equal:
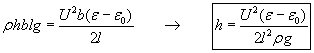
Let’s calculate the numerical values for two examples. When the dielectric is transformer oil:
r =860 kg/m3; er=2.2; l=5mm; U=30 kV; then the height of the liquid column: h=2.26 cm.
When the dielectric is glycerin:
r =1270 kg/m3; er=56 (at 15 deg. Celsius); l=5mm; U=30 kV; then the height of the liquid column: h=70.4 cm.
The higher dielectric constant of the glycerin naturally produces greater electric pressure at the edges, and therefore the liquid goes much higher between the plates than in the case of oil. After proper calibration this device can be also used for measuring high voltage.

