-
Conversion of energy forms

- Coût du kwh électrique
- Energy production
- Energy consumption
- Worldwide energy resources
- The sustainable development
- Energy and its various forms
- Conversion of energy forms
- Efficiency of processus
- Green energy plants
- Force conservative et énergie
- Over-unity and conversion process
- Amplify the inlet energy
- Modes de production d'énergie
- Production d'énergie et pollution
- Edition
-
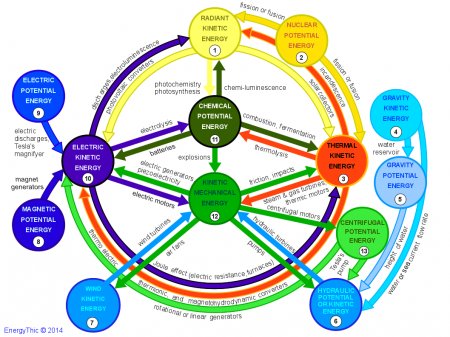
Conversion of energy forms
The various conversion processes
Click to see a magnified picture
Different ways to create excess energy
Reminder of the energy conservation law
ΔE = ΔU + ΔEk + ΔEp = ΔQ in + ΔQ out + ΔQ out losses + ΔW int + ΔW out + ΔW in (1) With :
ΔE : overall energy variation of the system, ΔU : variation of internal energy, ΔEk : variation of kinetic energy, ΔEp : variation of potential energy, ΔQ in : heat received by the system from external medium, ΔQ out : heat transfered by the system to external medium ΔQ out losses : worsened heat (friction losses) transfered by the system to external medium ΔW int : work of internal forces other than losses generated by energy conversion process, ΔW in : work of external forces input into the system, ΔW out : work output by the system.
Mechanical engine amplifying inlet energy
Let us consider the case of a machine operating at a stable and constant rotation speed, and for which no potential, kinetic or internal energy variation can be recorded between times t and t ', t ' being later than t. The produced work is consumed by a load.
ΔU = ΔEk = ΔEp = 0 Then : ΔE = ΔU + ΔEk + ΔEp = 0 We suppose that no heat is exchanged, except of worsened heat, between the machine and the external medium. Then, it comes :
ΔQ in = ΔQ out = 0 With these assumptions, equation (1) becomes :
ΔQ out losses + ΔW int + ΔW out + ΔW in = 0
ΔW out = - ΔQ out losses - ΔW int - ΔW in
By convention, the work brought to the input of the machine [ ΔW in ], and disbursed for the operator, is counted negatively. The work provided at the output of the machine is counted positively.
| ΔW out | = - ΔQ out losses - ΔWint + | ΔW in |
In some identified cases when machines are cleverly engineered, the work of internal forces can be negative and is added to the work provided at the inlet of the machine. But of course, part of the internal work created by friction losses still remains positive, that reduces the outlet work of the machine.
ΔWint < 0
ΔW int friction losses = - ΔQ out losses > 0 => the friction losses are entirely converted into worsened heat.
| ΔW out | = | ΔQ out losses | + | ΔW int | + | ΔW in | And the coefficient of energy [COE] is equal to :
COE = Σ E out / Σ E in = [ | ΔQ out losses | + | ΔW int | + | ΔW in | ] / | ΔW in |
The useful outlet energy is equal to : | ΔW out useful | = | ΔW int | + | ΔW in |
The efficiency is equal to ratio : η = Σ E out useful / Σ E in = [ | ΔW int | + | ΔW in | ] / [ | ΔQ out losses | + | ΔW int | + | ΔW in | ]
Then : η = | ΔW out useful | / [ | ΔQ out losses | + | ΔW out useful | ]
And :
COE = Σ E out / Σ E in = [ | ΔQ out losses | + | ΔW out useful | ] / | ΔW in |
COE = [ | ΔW out useful | * (1-η) / η + | ΔW out useful | ] / | ΔW in |
COE = [ (1-η) / η + 1 ] * | ΔW out useful | / | ΔW in
COE = (1 / η) | ΔW out useful | / | ΔW in
COE = (1 / η) | ΔW out useful | / | ΔW in Let's calculate COP ratio
COP = Σ E out useful / Σ E in operator = | ΔW out useful | / | ΔW in = [ | ΔQ out losses | + | ΔW int | + | ΔW in | ] / | ΔW in |
COP = | ΔW out useful | / | ΔW in
We can then write COE as follows :
COE = (1 / η) COP > COP > 1 We see in this example of energy conversion process, not using a thermodynamic Carnot type cycle, that COE coefficient defines the energy amplification of the machine, including worsened heat rejected at outlet, while the COP coefficient defines the ratio of net energy recovered to energy expended by operator at input.
Case of heat pump - relationship between efficiency, COP and COE
We suppose that heat pump operates at stable run. One can write :
ΔU = ΔEk = ΔEp = 0 Then : ΔE = ΔU + ΔEk + ΔEp = 0 There is no energy amplification of the machine : | ΔW in | = 0.
With these assumptions, equation (1) becomes :
| ΔQ out | + | ΔQ out losses | - | ΔQ in | - | ΔW in | = 0 =>
| ΔQ out | + | ΔQ out losses | = | ΔQ in | + | ΔW in |
COE = Σ E out / Σ E in = [ | ΔQ out | + | ΔQ out losses | ] / [ | ΔQ in | + | ΔW in | ] = 1
COE = 1 Let's calculate COP coefficient :
COP = Σ E out useful / Σ E in = | ΔQ out | / | ΔW in | = [ | ΔQ in | + | ΔW in | - | ΔQ out losses | ] / | ΔW in |
The efficient of the machine is equal to : η = | ΔQ out | / [ | ΔQ out losses | + | ΔQ out | ] = | ΔQ out | / [ | ΔQ in | + | ΔW in | ]
And : COP = COE - η . | ΔQ out losses | / | ΔQ out |
Amplify the energy within a machine => COE (coefficient of energy) > 1
In some identified cases when machines are cleverly engineered, the work of internal forces can be negative and it adds to the work provided at the inlet of the machine. But of course, part of the internal work created by friction losses still remains positive, that reduces the outlet work of the machine.
Then : | ΔWint | < 0
and | ΔWint friction losses | > 0
Let's write the complete equation in that case :
| ΔWoutlet| = | ΔWinlet | - | ΔWint friction losses | + | ΔWinlet |
COE = | ΔWoutlet | / | ΔWinlet | = [ | ΔWinlet | + | ΔWint | - | ΔWint friction losses | ] / | ΔWinlet |
COE = 1 + [ | ΔWint | - | ΔWint friction losses | ] / | ΔWinlet |
We will assume that | ΔWint | is much greater than | ΔWinlet |. | ΔWint | / | ΔWinlet | = k >>1. Furthermore, as usual, | ΔWint friction losses | is negligible compared to | ΔWinlet |. Then :
COE = 1 + [ | ΔWint | - | ΔWint friction losses | ] / | ΔWinlet | = 1 + k - | ΔWint friction losses | / | ΔWinlet |
COE = 1 - | ΔWint friction losses | / | ΔWinlet | + k = η + k > 1
1+k > COE = | ΔWoutlet | / | ΔWinlet | = η + k > 1 with η = efficiency and k much greater than 1 The internal friction losses drop down the efficiency of the machine and then the global COE whereas the other internal forces increases the COE over unity.